예전에 <화성학>을 배울 때 들었던 말인데, 당시 선생의 설명이 만족스럽지 않아 찾아봤던 단어.
그래도 만족스럽지 않았던.
그 후에 여기에도 독후감을 적었던 음악에 대해 과학적으로 쉽게 설명한 <음악의 비밀>에서 약간 이해가 됐던 것도 같은 데 아직도 이해가 잘 않된다.
며칠 전 색소폰카페에 보니, 이 단어에 대한 설명이 두 글에 걸쳐서 있는데 이해가 안되고 낯설다.
그래서 다시 ,위키디피아>를 찾았다.
(Wikidepea) 정말 얼마나 대단한 발명인가!
여기에도 나오지만, 옛날 어릴 때에는 피타고라스가 왜 음악이론을 연구했는 지를 이해하지 못했다.
여기 보니 헬름홀츠의 이름도 나온다.
이렇듯 한시대를 앞서 갔던 자들이 왜 이런 음악적 이론에 대해 얘기했을까?
이제야 이해할 듯 하다.
이들은 왜 음악이 우리에게 관심의 대상이 되고, 왜 우리의 좋은(!) 감정을 불러 일으키냐에 (즉, 즐겁게 들리는 소리, "음""악") 궁극적인 관심을 가지고 소리와 음악과 악기의 관련성을 이론적으로 연구했던 것 같다.
내가 지금 뒤늦게 나마, 다시 <다이아토닉 스케일>이나 <퍼펙트5th> 니를 찾아 보는 것과 같은 맥락에서 말이다.
이들도 음악연주를 했을까?
색소폰 연주가 아닌 것은 확실한데.
아니면 노래를 했을까?
잘 했을까?
한번 찾아봐야겠다.^^
(From Wikidepea)
Diatonic scale
| This article needs additional citations for verification. (June 2013) |
| Qualities | |
|---|---|
| Number of pitch classes | 7 |
In music theory, a diatonic scale (or heptatonia prima) is a scale composed of seven distinct pitch classes. The diatonic scale includes five whole steps and two half steps for each octave, in which the two half steps are separated from each other by either two or three whole steps, depending on their position in the scale. This pattern ensures that, in a diatonic scale spanning more than one octave, all the half steps are maximally separated from each other (i.e. separated by at least two whole steps). The word "diatonic" comes from theGreek διατονικός, meaning progressing through tones.[1]
The seven pitches of any diatonic scale can be obtained using a chain of six perfect fifths. For instance, the seven natural pitches which form the C-major scale can be obtained from a stack of perfect fifths starting from F:
- F—C—G—D—A—E—B
Called Pythagorean tuning, this property of the diatonic scales was historically relevant and possibly contributed to their worldwide diffusion because for centuries it allowed musicians to tune musical instruments easily by ear.
Any sequence of seven successive natural notes, such as C-D-E-F-G-A-B, and any transposition thereof, is a diatonic scale. Piano keyboards are designed to play natural notes, and hence diatonic scales, with their white keys. A diatonic scale can be also described as two tetrachords separated by a whole tone.
The term diatonic originally referred to the diatonic genus, one of the three genera of the ancient Greeks. In musical set theory, Allen Forte classifies diatonic scales as set form 7–35.
Perfect fifth
| Inverse | perfect fourth |
|---|---|
| Name | |
| Other names | diapente |
| Abbreviation | P5 |
| Size | |
| Semitones | 7 |
| Interval class | 5 |
| Just interval | 3:2 |
| Cents | |
| Equal temperament | 700 |
| 24 equal temperament | 700 |
| Just intonation | 702 |
In music theory, a perfect fifth is the musical interval corresponding to a pair of pitches with a frequency ratio of 3:2, or very nearly so.
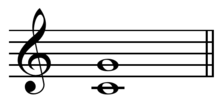
In classical music from Western culture, a fifth is the interval from the first to the last of five consecutive notes in a diatonic scale.[1] The perfect fifth (often abbreviated P5) spans seven semitones, while the diminished fifth spans six and the augmented fifth spans eight semitones. For example, the interval from C to G is a perfect fifth, as the note G lies seven semitones above C.![]() Play (help·info)
Play (help·info)
The perfect fifth may be derived from the harmonic series as the interval between the second and third harmonics. In a diatonic scale, thedominant note is a perfect fifth above the tonic note.
The perfect fifth is more consonant, or stable, than any other interval except the unison and the octave. It occurs above the root of allmajor and minor chords (triads) and their extensions. Until the late 19th century, it was often referred to by one of its Greek names,diapente.[2] Its inversion is the perfect fourth. The octave of the fifth is the twelfth.
A helpful way to recognize a perfect fifth is to hum the starting of "Twinkle, Twinkle, Little Star"; the pitch of the first "twinkle" is the root note and pitch of the second "twinkle" is a perfect fifth above it.
여기서 보면 P5라는 것은 기본음에서 찾기가 쉬운 듣기좋은(?!) 음이라서 중요한 것이다.
(왜 찾기가 좋으냐면, 귀에 듣기가 좋으니 특별한 기구가 없이도 귀로 할 수 있는 <피타고라스 튜닝>을 할 수가 있기 때문이다.)
unison (In music, unison is two or more musical parts sounding the same pitch or at an octave interval, usually at the same time.
Rhythmic patterns which are homorhythmic are also called unison.[1]: 즉, 같은 음) 과 octave (In music, an octave (Latin: octavus: eighth) or perfect octave is the interval between one musical pitch and another with half or double its frequency. It is defined by ANSI[1] as the unit of frequency level when the base of the logarithm is two. The octave relationship is a natural phenomenon that has been referred to as the "basic miracle of music", the use of which is "common in most musical systems".[2] : 즉 주파수가 배 이거나 반 인 음)이 음악에서 제일 안정된 관계이고, 그 다음으로 안정된 음이 바로 이 P5 음이라는 것이다.
왜?
P5관계는 기초음과 완전5도 간격으로 이루어진 음으로 물리적으로는 아래음이 3번 떨 때 윗음은 2번 떠는 (데 아주 가까운) 관계이다.
이런 물리적인 관계에 있기 때문에 우리 귀에 (반복되는 패턴을 찾지 못하는?!, 즉 알 수 없는) 소음으로 들리지 않고 (반복되는 주파수 패턴으로 인식되는, 즉 알 수 있는) 화음으로 들리는 것이다.
그리고 주어진 음 하나에서 이런 P5 관계로 주어진 옥타브 안의 나머지 여섯 음을 모두 차례로 찾을 수 있기 때문에 <다이아토닉 스케일>이 중요한 것이다.
왜냐 하면 어떤 음을 생성하더라도 그 음에 어울리는 다른 P5 관계에 있는 <natural> 음을 옥타브 내에서나 아래 위 옥타브 안에서 찾을 수 있고 그것은 음향적으로 어울리는 음이기 때문에 <dia-tonic>이라고 불리는 것이다.
그리고, 그래서 다이아토닉 스케일이 유용한 것이다.
<질문: 그럼 펜타토닉 스케일도 다이아토닉 스케일인가? >
전자의 universality를 생각한다면, 당연히 그래서 널리 퍼지고 살아남은 음악시스템이라고 생각되지만,
위에서 읽을 수 있는 다이아토닉 스케일의 정의에서 서양음악에서는 7음계를 가정하고 있다.
그러면, 옥타브는 <harmonics>에서 <even 배음>으로 볼 수 있고, P5는 <odd 배음>으로 볼 수 있을 것 같다.
보통 even배음은 귀에 거슬리지 않고, odd배음은 귀에 상대적으로 거슬린다고 하는데...
순수한 정현(sine)파를 포함해서 모든 음은 기초음과 배음들의 가중치의 합인 배열로 표현될 수가 있고, 이들 배음들의 가중합의 차이로 주어진 음파의 고유한 음색이 정해지는 것이다.
'색소폰 연주' 카테고리의 다른 글
| [스크랩] Re:Pentatonic? (0) | 2015.12.27 |
|---|---|
| 2015. 12. 24: 돌아와요 부산항 (외우기) 연습 (0) | 2015.12.24 |
| [스크랩] 단조 와 장조에 차이 (0) | 2015.12.14 |
| [스크랩] 장조와 단조의 식별 (0) | 2015.12.14 |
| [스크랩] 장조와 단조 구별법]- (0) | 2015.12.14 |